フルサイズがAPS-Cよりもボケるって本当？それはなぜ？––レンズの焦点距離によるボケ量の違いを計算してみよう

フルサイズはよくボケる？

写真を撮る人なら誰もが聞いたことがあるでしょう。「フルサイズのカメラは，APS-Cよりもよくボケる」。さて，これは本当でしょうか？

答えは…ある意味では間違い，ある意味では本当です。

「ある意味では間違い」というのは「同じ光学系（レンズ）を使った場合，ボケの絶対量は変わらない」ということです。

また「ある意味では本当」というのは，「同じ画角で写真を撮った時に，大きなボケが得られる」ということです。

これらのことについては，このあと順を追って説明して説明していきますが，センサーサイズが大きいからボケが大きいわけではないのですね。

もう少し踏み込んでみましょう。

「フルサイズがよくボケるのは，同じ画角で写真を撮る時に，APS-Cよりも長い焦点距離のレンズを使うから」と理解している人もいるかもしれません。これはおおむね正解なのですが，実は説明としては不十分です。そして僕の知る限り，その先の説明をしている本やWebサイトは見たことがありません。

この記事では，焦点距離とボケの量の関係を詳しく考察します。そして「フルサイズはよくボケる」ことの本当の理由を明らかにしようと思います。

フルサイズはよくボケる？
同じ光学系（レンズ）なら，フルサイズでもAPS-Cでもボケの絶対量は同じ
同じ画角で写真を撮るには？
焦点距離1.5倍のレンズで写すとボケの大きさは…？
ボケの量の計算式を思い出してみよう
フルサイズのボケはAPS-Cの2.25倍以上になる（レンズの焦点距離によって変化する）
前ボケの大きさはどうなる？
いったんここまでをまとめてみよう
ボケの絶対量を含めたグラフを描いてみよう
レンズの焦点距離によるボケ量の違い
センサーサイズが小さい時
まとめ

同じ光学系（レンズ）なら，フルサイズでもAPS-Cでもボケの絶対量は同じ

これはもう見出しの通りです。同じレンズを使えば，当然のことながら，ボケの大きさを含めて同じ画像が得られます（ただし同じ焦点距離，絞り値のレンズでも，フルサイズ用とAPS-C用ではイメージサークルの大きさが違います）。

けれどもフルサイズとAPS-Cでは，その画像を映し出すセンサーのサイズが違います。したがって，同じレンズを使った場合，APS-Cで撮った場合に得られる写真は，フルサイズで撮った画像をトリミングしたものと同一となります（図1）。

さて，こうして得られた画像を同一の大きさのディスプレイやプリントに表示したとしましょう。この時，イメージセンサーに記録された画像が拡大されるわけですが，フルサイズセンサーはAPS-Cよりも1.5倍大きなサイズを持っているので，APS-Cでとった写真はフルサイズに比較すると，相対的に1.5倍大きく拡大されます。この時，ピントの合った被写体だけでなく，ボケも引き伸ばされます。したがって，出来上がった写真を比べると，ディスプレイまたはプリントの上では，APS-Cで撮った写真の方が，フルサイズで撮ったものよりも1.5倍大きなボケを持ったものになります。…意外でした？

同じ画角で写真を撮るには？

でも先ほどの図1を見ると明らかなように，同じレンズを使って写真を撮ると，フルサイズの場合，より広い範囲が写ります。言い換えれば被写体が小さく写るということです。これでは同じレンズを使ったとはいっても，「同じ写真をとった」とは言えませんよね。

じゃあ，フルサイズのカメラで，被写体をAPS-Cで撮った時と同じ大きさに写すにはどうすればいいでしょう？…その方法は2つあります。

被写体に近づいて写す
焦点距離が1.5倍長いレンズを使う

方法1では被写体と背景の距離感が変わってしまうので，一旦除外して考えることにします。被写体を同じ大きさで写そうとするなら，通常とる方法は2ですね。

例えばAPS-C カメラの「標準レンズ」というと，通常焦点距離が35 mm程度のものになります。だからフルサイズの場合，これと同じ画角のレンズは 35 x 1.5 = 52.5 mm の焦点距離です。なぜ1.5倍かというと，センサーサイズが1.5倍だからです。

実際には52.5 mmの単焦点レンズというのは販売されていないので，50 mmか55 mmがフルサイズの標準レンズになるわけですね。これらのレンズを使えば，APS-Cで35 mmを使った時とほぼ同じ画角の写真が撮れることになります。

焦点距離1.5倍のレンズで写すとボケの大きさは…？

ということで，フルサイズのカメラに焦点距離が1.5倍のレンズをつけて写真を撮ったとしましょう。この時得られる被写体の像の絶対的な大きさ（センサー上での大きさ）は，APS-Cの時の1.5倍です。そしてセンサーサイズも1.5倍ですから，出来上がる写真の上で，被写体は同じ大きさになります。

それではこの時，ボケの大きさは何倍になるでしょう？焦点距離が1.5倍だから，ボケの大きさも1.5倍？…だとすると，写真をPCのディスプレイに映し出した時（またはプリントした時），ボケの大きさはできあがった写真の上でAPS-Cと同じになるんじゃない？

…あれ？何だかおかしいですね。

ボケの量の計算式を思い出してみよう

さて，前記事「ボケの量を定量的に計算してみよう––35 mm F1.8の単焦点レンズと16–70 mm F4のズームレンズの比較を中心に」で，背景ボケの大きさCとレンズの焦点距離f，絞り値A，被写体および背景とレンズとの距離（それぞれDおよびD'）との間には，以下の関係があることを書きました（式1。この式の導出については前記事をお読みください）。

$C=\dfrac{f}{A}\cdot \dfrac{f\left( D'-D\right) }{D'\left( D-f\right) }$ …(1)

www.sunsunfine.com

この式に基づいて考えてみましょう。

フルサイズのカメラで，APS-Cと同じ画角の写真を撮った場合…つまり焦点距離が1.5倍のレンズを使って撮影した場合，ボケの大きさがどれくらいになるかは，式1で f のところに 1.5f を入れれば計算できます（式2）。

$C=\dfrac{1.5f}{A}\cdot \dfrac{1.5f\left( D'-D\right) }{D'\left( D-1.5f\right) }$ …(2)

このとき背景ボケの絶対量は，APS-Cの時の何倍になるでしょう？これは，APS-Cとフルサイズのボケ量をそれぞれ C_APS，C_FFとすると，C_FF/C_APSで求められます。計算してみましょう。式1 および式2から

\begin{aligned}\dfrac{C_{\mathrm {FF}}}{C_{\mathrm{APS}}}=\left[ \dfrac{1.5f}{A}\cdot \dfrac{1.5f\left( D'-D\right) }{D'\left( D-1.5f\right) }\right] /\left[ \dfrac{f}{A}\cdot \dfrac{f\left( D'-D\right) }{D'\left( D-f\right) }\right] \\[3ex] =\dfrac{1.5f}{A}\cdot \dfrac{A}{f}\cdot \dfrac{1.5f\left( D'-D\right) \cdot D'\left( D-f\right) }{D'\left( D-1.5f\right) \cdot f\left( D'-D\right) }\\[3ex] \color{red}{=\left( \dfrac{1.5f}{f}\right) ^{2}\cdot \dfrac{\left( D-f\right) }{\left( D-1.5f\right) }} \,\,\,\,\,\,\,\,…(3')\\[3ex] \color{red}{=2.25\times \dfrac{D-f}{D-1.5f}} \,\,\,\,\,\,\,\,…(3)\end{aligned}

このように，式3からは D' が消えてしまっています。またこの式3からわかるように，ボケが何倍になるかは被写体までの距離 D と焦点距離 f に依存しますが，例えばAPS-Cとフルサイズのカメラの焦点距離fがそれぞれ35 mmと52.5 mmで，被写体までの距離D が5 m（5000 mm）の時は

$\dfrac{C_{\mathrm {FF} \, \left( 52.5\, \mathrm {mm}\right) }}{C_{\mathrm {APS}\, \left( 35\, \mathrm {mm}\right) }}=2.25 \times \dfrac{5000-35}{5000-52.5}=2.2511\ldots$

より，フルサイズはAPS-Cに対して，絶対量にして約2.25倍の大きさのボケを与えるということになります。センサーサイズは1.5倍ですから，プリントした写真上でのボケの大きさは，2.25 ÷ 1.5 = 1.5 より，約1.5倍になるということですね。

フルサイズのボケはAPS-Cの2.25倍以上になる（レンズの焦点距離によって変化する）

ここでもう一度式3 を見てみましょう（下にもう一度示します）。

\begin{aligned}\dfrac{C_{\mathrm {FF}}}{C_{\mathrm{APS}}} \color{red}{=2.25\times \dfrac{D-f}{D-1.5f}} \,\,\,\,\,\,\,\,…(3)\end{aligned}

この式において D が f に比べて十分に大きい時（カメラと被写体の距離がレンズの焦点距離に比べてずっと長い時），(D – f)/(D – 1.5f) ≒ 1 となります。するとC_FF/C_APS ≒ 2.25 ですから，フルサイズで撮った写真はAPS-Cに比べて約2.25倍の大きさのボケを与えることになります（出来上がった写真の上では約1.5倍の大きさのボケ）。先ほど計算してみたのはこのケースに当てはまります。

ちなみに2.25という数字は，1.5の2乗です。つまり被写体が十分に遠い場合，ピントの合った被写体の像の絶対的な大きさは焦点距離の1乗に比例するのに対して，ボケの大きさは焦点距離の2乗に比例するのです。このことは式3を約分しきる前の形，式3' を見ると容易に理解できます（もう一度示します）。

\begin{aligned}\dfrac{C_{\mathrm {FF}}}{C_{\mathrm{APS}}} \color{red}{=\left( \dfrac{1.5f}{f}\right) ^{2}\cdot \dfrac{\left( D-f\right) }{\left( D-1.5f\right) }} \,\,\,\,\,\,\,\,…(3')\end{aligned}

このことこそが「APS-Cよりもフルサイズの方がよくボケる」ことの本当の理由なのです。

またフルサイズとAPS-Cの比較のように，レンズの焦点距離とセンサーサイズを同じ割合で変化させた場合には，できあがった写真上の見かけの大きさを考えると，被写体の像の大きさには，焦点距離が0乗で効き (1.5⁰ = 1)，ボケの大きさには焦点距離が1乗で効いてくることになります。

一方，D と f がある程度近い値になってくると（被写体の近くから撮影する or 焦点距離の長いレンズを使った時がこれに相当します。望遠マクロが典型例ですね），(D – f)/(D – 1.5f) は1よりも有意に大きな値をとるので，フルサイズのボケはAPS-Cの2.25倍よりもさらに大きくなっていきます。

図2 被写体までの距離Dを固定して同じ画角で撮影した時，焦点距離によってフルサイズのボケの相対サイズ [APS-Cの何倍か] がどのように変化するか

図2はD（カメラと被写体との間の距離）を固定した時，焦点距離によって C_FF/C_APS がどのように変化するかを示しています。横軸はAPS-Cの焦点距離＆フルサイズの焦点距離です。この図は，レンズの焦点距離が短い時 C_FF/C_APSは2.25に近い値をとるのに対して，焦点距離が長くなっていくとこの値が急激に大きくなっていくことを明確に示しています。

例えば 2 m（2000 mm）先の被写体を撮った時，使ったレンズがAPS-Cで200 mm／フルサイズで300 mm なら，以下の計算から，フルサイズの写真はAPS-Cの約2.38倍（出来上がった写真の上では見かけ上約1.59倍）のボケを与えることがわかります。

$\dfrac{C_{\mathrm {FF} \, \left( 300\, \mathrm {mm}\right) }}{C_{\mathrm {APS}\, \left( 200\, \mathrm {mm}\right) }}=2.25 \times \dfrac{2000-200}{2000-300}=2.3823\ldots$

いずれにしても，同じ画角で写真を撮った時，フルサイズのカメラは，APS-Cに比べて絶対量で少なくとも2.25倍以上（出来上がった写真上で1.5倍以上）の大きさの背景ボケを与えることがわかりました。

前ボケの大きさはどうなる？

前ボケの大きさC'とレンズの焦点距離f，絞り値A，被写体および前景とレンズとの距離（それぞれDおよびD"）との間には，以下の関係が成り立ちます（式4。この式の導出についても前記事をお読みください）。

$C'=\dfrac{f}{A}\cdot \dfrac{f\left( D-D''\right) }{D''\left( D-f\right) }$ …(4)

「フルサイズのカメラでAPS-Cと同じ画角で写真を撮った場合，何倍の大きさのボケが得られるか」は，先ほどと同様に，以下の計算（式5）で求められます。フルサイズとAPS-Cの前ボケの絶対量をそれぞれC'_FF, C'_APSとすると

\begin{aligned}\dfrac{C'_{\mathrm {FF}}}{C'_{\mathrm{APS}}}=\left[ \dfrac{1.5f}{A}\cdot \dfrac{1.5f\left( D-D''\right) }{D''\left( D-1.5f\right) }\right] /\left[ \dfrac{f}{A}\cdot \dfrac{f\left( D-D''\right) }{D''\left( D-f\right) }\right] \\[3ex] =\dfrac{1.5f}{A}\cdot \dfrac{A}{f}\cdot \dfrac{1.5f\left( D-D''\right) \cdot D''\left( D-f\right) }{D''\left( D-1.5f\right) \cdot f\left( D-D''\right) } \\[3ex] \color{red}{=2.25\times \dfrac{D-f}{D-1.5f}} \,\,\,\,\,\,\,\,…(5)\end{aligned}

得られる関係は，先ほどの背景ボケの時（式3）と全く同じです。つまり前ボケに関しても，フルサイズはAPS-Cの2.25倍以上のボケを与え（画面上の見かけのボケ量は1.5倍以上），レンズの焦点距離が長くなると，ボケの拡大の割合も大きくなっていくということですね。

いったんここまでをまとめてみよう

ここまでをいったんまとめると，以下のようになります。

フルサイズのカメラを使って，APS-Cの時と同じ画角の写真を撮るには，1.5倍の焦点距離のレンズを使う必要がある
すると，被写体の像の絶対的な大きさは1.5倍になる（プリントした画面の上では同じ大きさになる）
これに対して，ボケの大きさは2.25倍またはそれ以上になる。したがってプリント上でのボケは1.5倍またはそれ以上になる
これは（特にレンズの焦点距離にに比較して，被写体までの距離が十分に遠い時）ピントの合った被写体の像の絶対的な大きさは焦点距離に比例するのに対し，ボケの大きさは近似的に焦点距離の2乗に比例するからである
フルサイズとAPS-Cにおけるボケの大きさの比率は，焦点距離が長くなったりレンズから被写体までの距離が短くなったりすると急激に大きくなる

これでフルサイズのカメラを使った時に，APS-Cよりも大きなボケが得られる理由がわかりましたね！

ボケの絶対量を含めたグラフを描いてみよう

ここまで，フルサイズのボケがAPS-Cの何倍になるかを議論してきました。それではボケの絶対量そのものを含めてグラフを描いてみましょう。ボケの絶対量（センサー上でのボケの大きさ）は，式1および式4を使えば算出することができます。

図3は，35 mmと52.5 mmのレンズ（それぞれAPS-Cとフルサイズの標準レンズ）を使い，絞りF1.8で2mのところにある被写体を撮った時，前景および背景がどの程度ボケるかを表しています。横軸がレンズから前景および背景までの距離，縦軸がボケの絶対量（単位：mm）です（「ボケが1 mm」というのは，本来点であるものがボケてセンサー上で 1 mmの大きさに写るということです）。

図3 35 mm (APS-C) および52.5 mm (フルサイズ)レンズを使った時のボケの絶対量

この図の中にC_FFとC_APSが描きこまれていますが，C_FF/C_APSは2.27です（C_FFとC_APSをどの位置で比較してもこの値になります）。ここでは被写体までの距離が2 mと比較的短いので，2.25 (1.5²) よりもやや大きい値になっています。

次に，できあがった写真上での見かけのボケの大きさも図にしておきましょう。図4は写真をA4サイズにプリントした時に，ボケが何mmになるかを示しています。

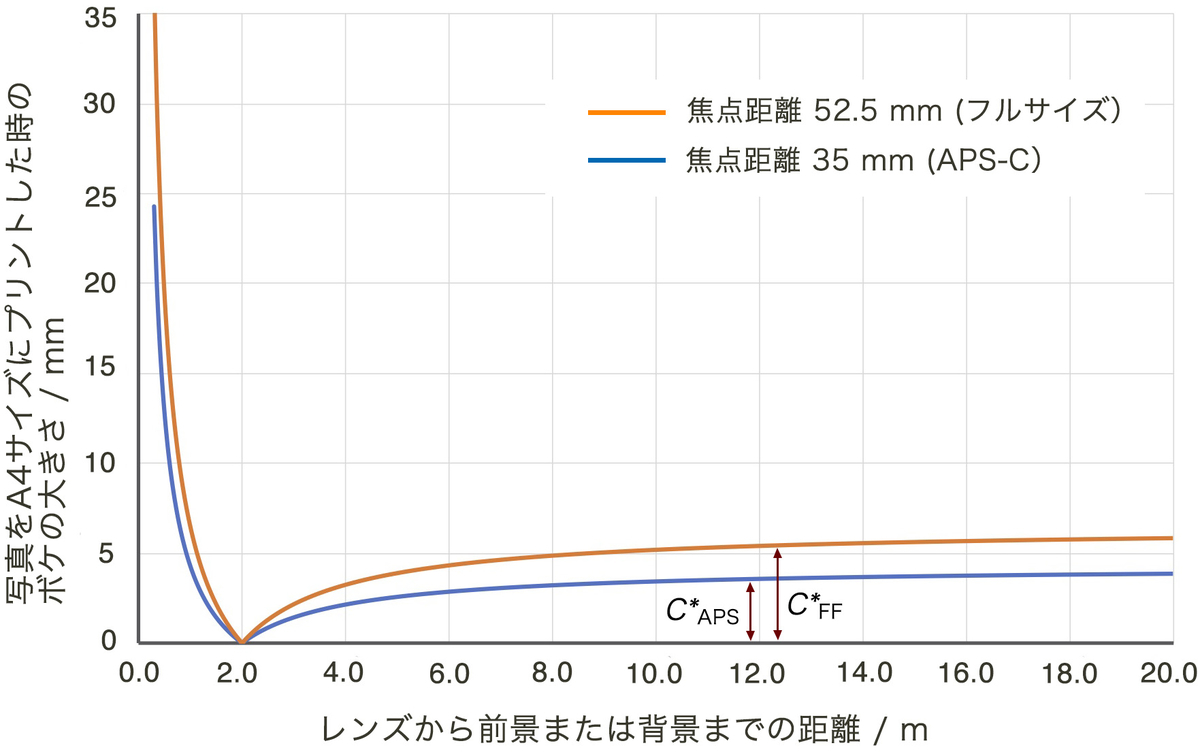
この時，フルサイズとAPS-Cにおける見かけのボケの大きさをそれぞれ C*_FFおよび C*_APS とすると，その比はどの位置で比較しても 1.51 になっています。

レンズの焦点距離によるボケ量の違い

最後に，焦点距離を変数とした時のボケ量の変化もグラフにしておきます。図5は 5 m 離れた被写体を撮った時に，無限遠の背景がどの程度ボケるかを示しています。横軸は焦点距離，縦軸がmm単位で表したセンサー上のボケ量です。

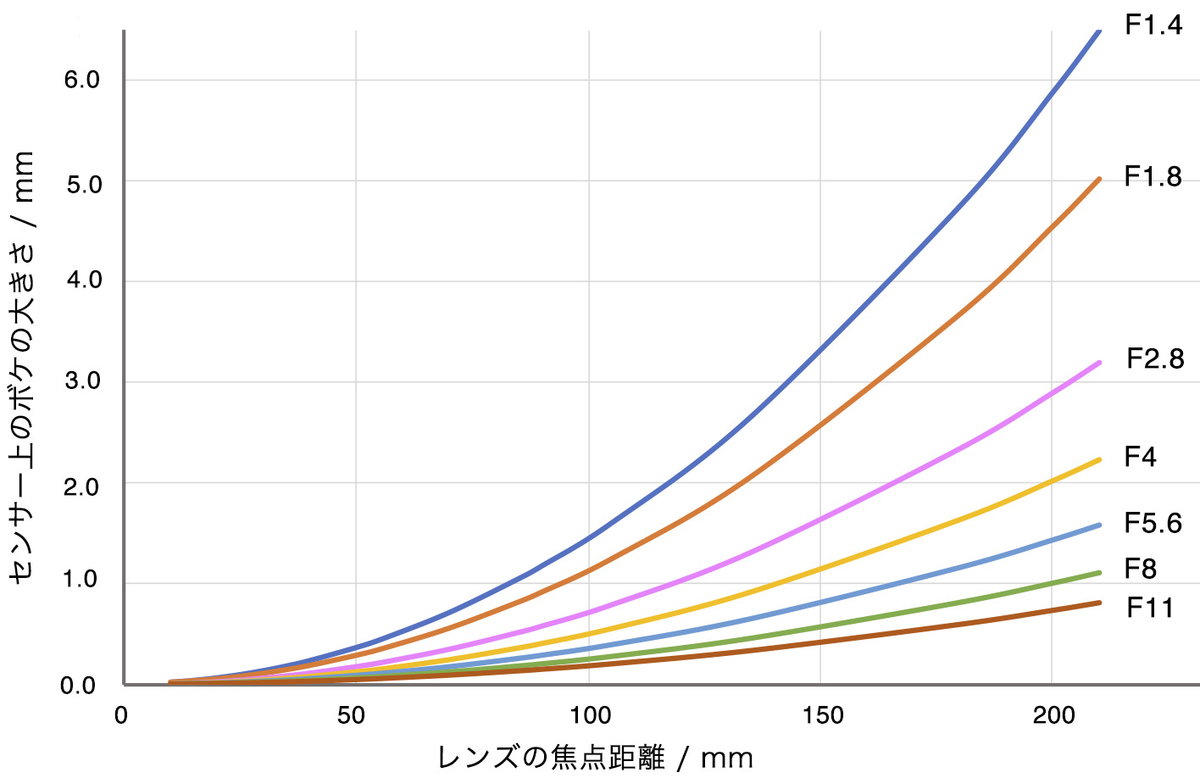
先に述べたように，ボケの量には焦点距離の2乗が効いてくるので，得られる曲線は二次曲線で近似されるものになっています（特に焦点距離が短い領域）。

このように，焦点距離が長くなるほどボケ量は急激に増えていきます。つまり「ぼかす時には絞りを開けるとよい」とよく言われますが，ボケの大きさにより強く効いてくるのは焦点距離です（式1および式4からわかるように，ボケ量は絞り値の1乗に反比例です）。…もちろん焦点距離を変えると被写体との距離感や背景との圧縮具合が変わって，全然違う写真になるので，「ボカしたければ焦点距離を長くしろ」というのはかなり乱暴な議論であることは承知していますが。

例えば下に示すように，焦点距離200 mmだとF8（APS-C）でもこれくらい大きなボケが得られます ↓。